Free42
Dette er en kort gennemgang af HP lommeregneren Free42. Det er en lommeregner der havde sin storhedstid i 90'erne, men som desværre (IMHO) tabte til texas lommeregnerne.
Du kan finde en digital udgave af den her: Digital udgave af HP42S
Manual: http://thomasokken.com/free42/42s.pdf
Hp15c : http://hp15c.com/
Den kan downloades på androind og IPhone, hvor den har navnet free42
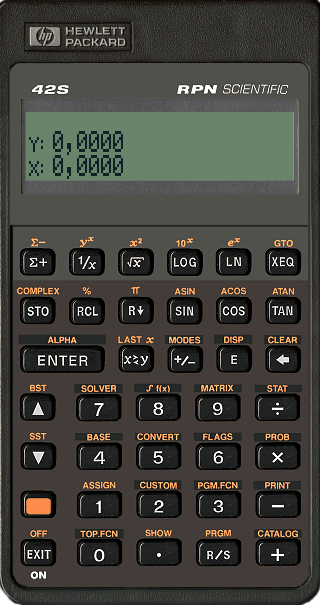
Hvad er forskellen
Forskellen er måden matematikken tænkes på, og det kan ses i følgende regnestykke
På en texas lommeregner skal man indtaslte
- 2 \( x^2 \) = → -4
Noget overraskende giver resultatet \( -4 \) - hvilket er forkert
Så prøver man at gøre det "rigtigt" ved at bruge lommeregnerens \( \pm \) taste (-)
2 (-) \( x^2 \) = → -4
... hvilket også er forkert
Endeligt prøver man følgende
( - 2 ) \( x^2 \) = → 4
Nu blev det endeligt rigtigt ... men hvad er forklaringen?
Årsagen til dette skal findes i måden som texaslommeregneren betrager led i matematiske sætninger - eller mere præcist, at lommeregnere opfatter + og - som de tegn der adskiller led. Derfor vil et indledende - blive tolket som adskiller af led. I dette tilgælde vil lommeregneren altså "læse" regnestykket:
Dette problem kan omgås ved RPN (Reverse Polish Notation), hvor man først skriver operatoren efter udtrykket
På free42 indtaster man følgende:
2 \( \pm \) ▮ \( x^2 \) → 4
- tal
- fortegn - "binder" sig til tallet i hukommelsen
- funktion ( orange selector for sekundær funktion
HP lommeregneren "tænker" altså ikke for dig, men gør kun det som du taster ind.
Hvordan fungerer det
Det som får denne lommeregner til at fungere er, at den kan have nogle tal i hukommelsen. For Free42 drejer det sig om 4 tal. Hver gang man trykker på ENTER eller en funktionstast så gemmer den tallet i hukommelsen.
Prøv at lave følgende løsning ved hjælp af det nummeriske keyboard (nummerisk keyboard som normalt.)
1 Enter 2 Enter 3 Enter 4
Det som lige er sket er, at vi har fyldt 4 hukommelsesceller op:
- 1
- 2
- 3
- 4
På lommeregneren står der:
Y: 3,000
X: 4
Hvis vi nu trykker på + vil der stå
Y: 2,000
X: 7,000
Den har altså taget de to tal i displayed og lagt dem sammen. Hvis vi kigger på vores hukommelse fra før, så ser den nu ud som nedenfor:
- 1
- 2
- 7
Ved at trykke 2 x + vil vi altså lægge 2 og 1 til, og samtidig rykke hukommelsescellerne ned.
Teknikken bag dette er meget fascinerende, men det som gør dette smart er, at vi kan udregne stykker på en helt anden måde f.eks:
1 ENTER 2 + 3 ENTER 4 - ÷
- Udregn første parantes
- Udregn anden parantes
- Divider parenteserne med hinanden
1 ENTER 2 +
3 ENTER 4 -
÷
På en texas lommeregner skulle der være skrevet følgende:
( 1 + 2 ) / ( 3 - 4 ) =Altså 12 tryk, mod 9 på HP-lommeregneren.
Brug numerisk keyboard
| Keyboard | lommeregner | Keyboard | Lommeregner |
|---|---|---|---|
| \( \Sigma + \) | F1 eller a | \( \Sigma - \) | Shift F1 eller Shift A |
| \( \frac 1x \) | F2 eller v | \( y^x \) | Shift F1 eller Shift V |
| \( \sqrt x \) | F3 eller q | \( x^2 \) | Shift F3 eller Shift Q |
| \( LOG \) | F4 eller o | \( 10^x \) | Shift F4 eller Shift O |
| \( LN \) | F5 eller l | \( e^x \) | Shift F5 eller Shift L |
| \( COS \) | c | \( ACOS \) | Shift C |
| \( SIN \) | s | \( ASIN \) | Shift C |
| \( TAN \) | t | \( ATAN \) | Shift T |
| \( \pi \) | p | ||
| Ændre fortegn | n | ||
| Alle decimaler | Shift . | ||
| Videnskabelig notation | E | ||
Et overblik over alle taster: https://github.com/ahlstromcj/free42-resources/blob/master/skins/keymap
Eksempler
Eksempel 1
1 ENTER 2 + 3 +
6
Eksempel 2
4 ENTER 5 + 3 x
27
Eksempel 3
2 ENTER 3 x \( \frac{ 1 }{ x } \) 2 x
0,3333
Eksempel 4
2 ▮ \( x^2 \) 4 ENTER 2 \( \pm \) x 6 x -
64
Eksempel 5
3 , 3 E 1 9 ENTER 1 9 ÷
1,7368E18
Opgaver
Opgave 1
26,26
Opgave 2
Beregn \( T_{24},~~ T_{102} \)
300; 5253
Opgave 3
Beregn nulpunkter og toppunkter i følgende andengradsligninger:
Formler
Opgave 4
Beregn \( F_{24}, ~~ F_{102} \)
46368; 9,2723E20 ( 9,2723 × 1010 )