Deskriptiv statistik

Begreber

Man anvender det ord der giver bedst mening.

Observation

Anvendes når der er noget specifikt man undersøger, f.eks. hvilke tøjmærker der er populære eller hvilke partier der bliver stemt på til et folketingsvalg. Man er aktivt opsøgende

Hændelse

Hændelser er noget som sker, noget konkret og som man registrer

Udfald

Når det handler om sandsynligheder og hvor det er chancebetonet, så taler man om udfald. Det kan f.eks. være terningkast eller antal rigtige på en lottokupon.

Udfaldsrum

Et udfaldsrum er de mulige udfald der kan forekomme. For et terningkast med en D6 terning er udfaldsrummet $ U = {1,2,3,4,5,6} $.

Population og stikprøve

Ofte har man ikke mulighed for at få det fulde datasæt, f.eks. ved en folkeafstemning hvor man anvender exit-polls. Her må man leve med at man kun har en delmængde af svar ud af helheden. Man har altså en stikprøve, der er taget fra en population. En population er alle data (100%).

Datasæt

Datasættet er de data man arbejder med.

Repræsentativ datasæt

Når en undersøgelse er repræsentativ betyder det at en stikprøve matematisk set giver et korrekt billede af populationen. At en statistik er repræsentativ kan afgøres ved hjælp af matematiske redskaber.

Kvalitatitve undersøgelser

Kvalitative undersøgelser fokuserer på detaljer der er svære at observere og måle. Det kan f.eks være holdninger. Det kan f.eks. ske ved observation eller interview

Kvantitative undersøgelser

Kvantitative undersøgelser fokuserer på detaljer der målbare og kan kvantificeres. Resultaterne kan bearbejdes statistisk og kan præsenteres numerisk. Det f.eks. ved spørgeskemaundersøgelser.

Diskret og kontinuert data

Når man har et datasæt skal man overveje hvordan det skal behandles, da det kan være forskelligt i forhold til den viden man gerne vil have. Se f.eks. på et folketingsvalg, hvor man både vil behandle tallene for de enkelte partier (diskrete observationer), men også for de politiske blokke (kontinuerte oberservationer) der går til valg.

Diskret data

Diskret data anvendes når der er tale om eksakte værdier og anvendes når der er en klar og logisk opdeling af data. Det kan f.eks. være ved:

Terningkast
Bilmærker
Partier ved valg
Tøjmærker
...

Kontinuert data

Nogle gange vil ens datasæt blive uoverskueligt ved at kun at arbejde med eksakte værdier. Data kobles sammen af en sammenhæng. Her vil man vælge at gruppere observationerne i nogle praktiske og anvendelige enheder. Det kan f.eks. være ved:

Højde målinger ( $ ]150;160], ]160;170[, ]170;180[, ]180;190[ ... $)
Aldersgrupper ($ ]18;23[, ]23;28[, ]28;33[ ... $)
...

Symboler

Symbol	Begreb	Definition	Talmængde
$ x $	Observation	Anvendt data
$ h(x) $	Hyppighed	Hvor ofte en observation/hændelse optræder	$ \mathbb{N}_0 $
$ H(x) $	Summeret hyppighed	Hvor ofte denne og forgående observationer/hændelser optræder	$ \mathbb{N}_0 $
$ f(x) $	Frekenvens	Hvor ofte en observation/hændelse optræder i forhold til det samlede antal observationer	$ \mathbb{R} $
$ F(x) $	Summeret frekenvens	Hvor ofte denne og forgående observationer/hændelser optræder i forhold til det samlede antal observationer	$ \mathbb{R} $

Et eksempel

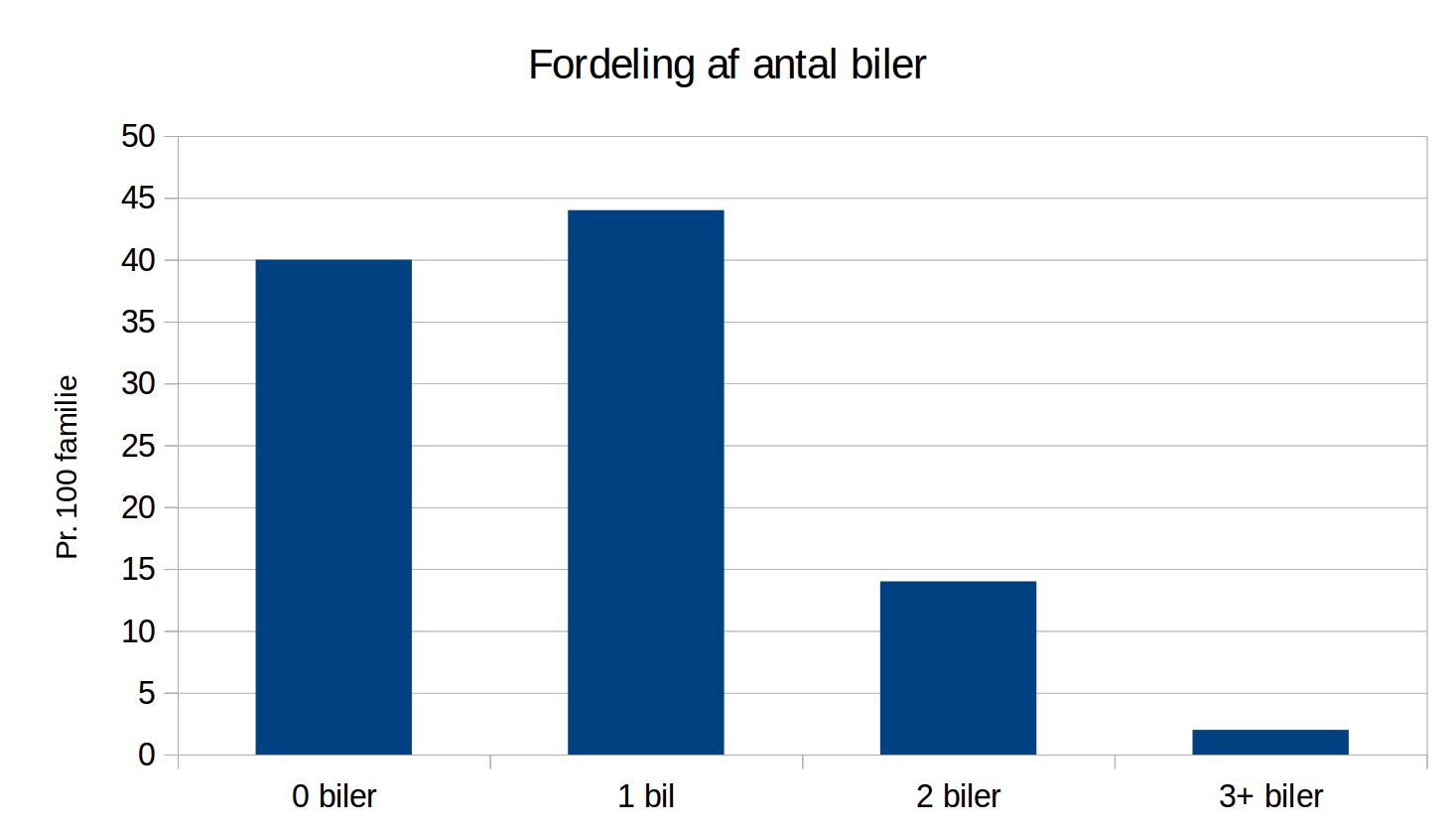
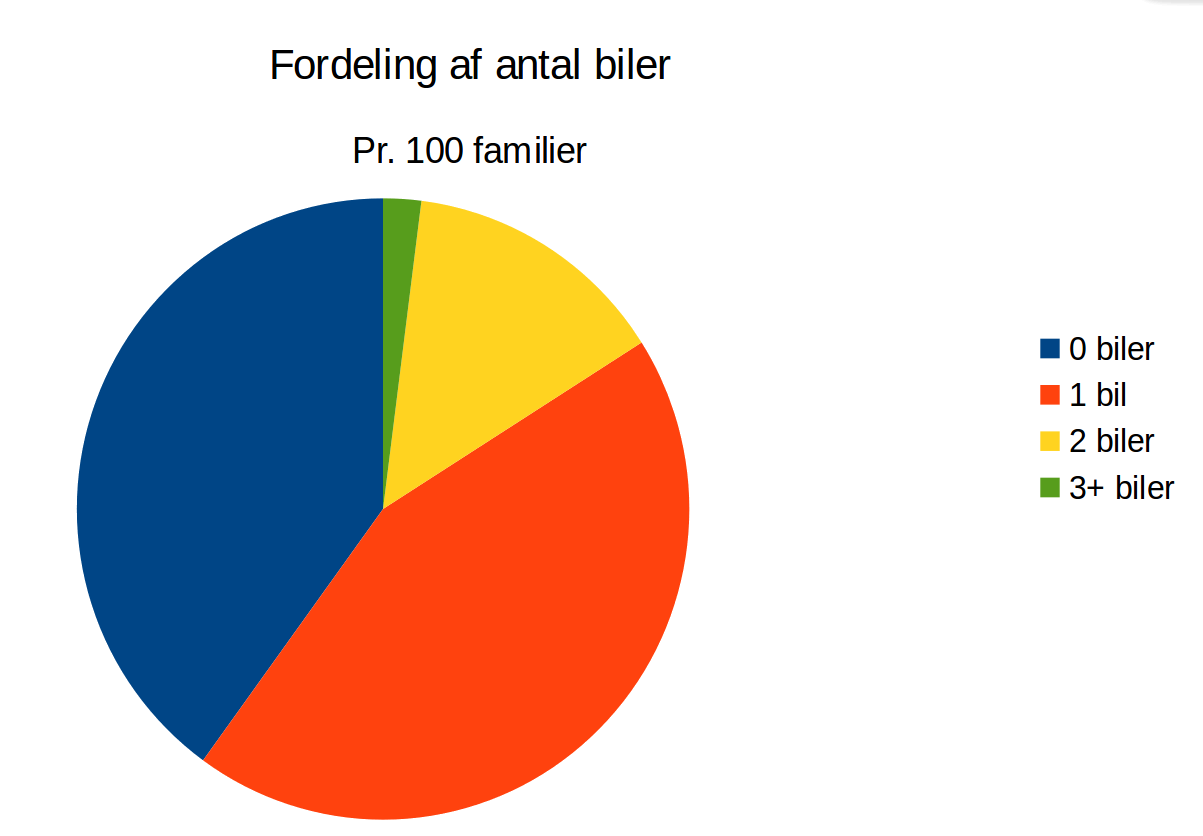
Forestil dig en tabel der angiver antal biler i en hustand

Antal biler ($ x $)	$ h(x) $	$ H(x) $	$ f(x) $	$ F(x) $
$ 0 $	$ 40 $	$ 40 $	$ 0,40 $	$ 0,40 $
$ 1 $	$ 44 $	$ 84 $	$ 0,44 $	$ 0,84 $
$ 2 $	$ 14 $	$ 98 $	$ 0,14 $	$ 0,98 $
$ 3+ $	$ 2 $	$ 100 $	$ 0,02 $	$ 1,00 $

Tallene er lavet ud fra Danmarks statistik for 2016: https://www.dst.dk/da/Statistik/emner/biler/familiernes-bilraadighed

Ved at anvende den summerede frekvens og hyppgihed, kan man beregne intervaller. Hvis man gerne vil finde frekvensen af antallet af familier der har 1 eller 2 biler anvender man følgende beregning:

$$ F(2)-F(0) = 0,98-0,40 = 58\% $$

Sandsynlighed

Sandsynligheden for en hændelse angives med $ P $ (Posibility). I forhold til skemaet begreberne ovenfor er der følgende sammenhænge:

$ P(X = x) $ er tilsvarende frekvensen $ f(x) $. Den kaldes også punktsandsynlighed.

$ P(X \leq x) $ er tilsvarende den summerede frekvens $ F(x) $.

Det som er forskellen mellem en frekvens og en sandsynlighed er, at sandsynligheder handler at kunne forudsige udfaldet af en situation. F.eks. hvad sandsynligheden er for at en familie har 1 eller 2 biler. Frekvensen er et udtryk for hvor mange der er i forhold til stikprøven.

Det ovenstående skema vil altså se ud som følger:

Antal biler ($ x $)	$ h(x) $	$ H(x) $	$ f(x) ~/~ P(X=x)$	$ F(x) ~/~ P(X \leq x)$
$ 0 $	$ 40 $	$ 40 $	$ 0,40 $	$ 0,40 $
$ 1 $	$ 44 $	$ 84 $	$ 0,44 $	$ 0,84 $
$ 2 $	$ 14 $	$ 98 $	$ 0,14 $	$ 0,98 $
$ 3+ $	$ 2 $	$ 100 $	$ 0,02 $	$ 1,00 $

Dvs. hvis man vil finde sandsynligheden af at en vilkårlig familie har 1 eller 2 biler, skal man anvende følgende beregning:

$$ P(X \leq 2) - P(X=0) = 0,98-0,40 = 58\% $$

Σ - opsummer

En af de notationsformer man anvender i statistik og sandsynlighed er $ \sum$, som betyder opsummer. Man skal simpelthen summere det som står efter $ \sigma $. Lod os kigge på en simpel tabel.

$ x_i $	$ h_i $	$ f_i $
1	1	0,1
2	4	0,4
3	2	0,2
4	3	0,2

Hvis vi skal beregne n (antal observationer) gøres det på følgende måde:

$$ n = 1+4+2+3 $$

Hvis man det generelt for den ovenstående tabel får man:

$$ n = h_1 + h_2 + h_3 + h_4 $$

Vi kan altså se vi skal skrive det samme hver gang, hvor det blot er selve $ h_i $ der skifter. Det kan vi notere som følgende ved hjælp af $ \sum $:

$$ n = \sum_{i=1}^4 h_i $$

Det som notationen fortæller er, at vi skal lade $ n $ gennemløbe værdierne fra $ 1 $ til og med $ 4 $, indsætte dem i udtrykket og og derefter opsummere resultaterne altså:

$$ n = \sum_{i=1}^4 h_i = h_1 + h_2 + h_3 + h_4 = 1+4+2+3$$

Herunder kigger vi på et datasæt der går fra i=1 → k (Det sidste tal der skal være med).

For at danne os et overblik over tabellen vælger vi at lave to rækker ($ x $ og $ x_i $). En hvor tallene står og en hvor vi angiver positionerne ved hjælp af værdierne $ x_1 $ til $ x_k $, hvor $ k $ er den sidste observation.

Generelt datasæt
$ x_i $	$ x_1 $	$ x_2 $	$ x_3 $	$ ... $	$ x_{k-2} $	$ x_{k-1} $	$ x_k$

Hvis vi ville opsummere tallene ville vi altså lave regnestykket: $ x_1+x_2+x_3+...+x_{k-2}+x_{k-1}+{x_k} $

Det kan som nedesstående, da vi skal opsummere $ x_i $-værdierne fra $ x_1 \rightarrow x_k $:

$$ \sum_{i=1}^{k} x_i = x_1+x_2+x_3+...+x_{k-2}+x_{k-1}+{x_k}$$

Statistiske deskriptorer

Aflæste deskriptorer

Deskriptor	Forklaring	Metode
Typetal (diskret data)	Den observation der forekommer flest gange	Aflæsning
Typeinterval (kontinuert data)	Den samling af observationer der er flest af	Aflæsning
Mindste værdi	Den mindst observerede værdi	Aflæsning
Største værdi	Den størst observerede værdi	Aflæsning
Median	Den midterste observation. Hvis der er et lige antal observationer er medianen gennemsnittet af de to midterste værdier.	Aflæsning
Middelværdi	Gennemsnit	Beregning

Anvendelse i regneark

Statistisk funktion	Beskrivelse
tæl(Område)	Antal observationer
tælv(Område)	Antal observationer (ikke tomme felter)
tæl.hvis(Område;Betingelse)	Antal observationer i området der opfylder betingelsen. Hvis betingelsen er et tegn skal det omgives med anførselstegn (f.eks: ") .
middel(Område)	Gennemsnit
min(Område)	Mindste værdi
maks(Område)	Største værdi
hyppigst(Område)	hyppigste værdi (Typetal)
median(Område)	Medianen
kvartil(Område;1/2/3)	Første, anden og tredje kvartil

Antal

Antallet af observationer i et datasæt beregnes medformlen:

$$ n = \sum_{i=1}^{k} h_i $$

Middelværdi (gennemsnit)

$$ \overline x = \sum_{i=1}^{k} x_i \cdot f_i $$

eller ( da $ f_i = \frac{1}{n} \cdot h_i $ ) :

$$ \overline x = \frac{1}{n} \cdot \sum_{i=1}^{k} x_i \cdot h_i $$

Kvartilsæt

For at danne sig et overblik over ens observationer ser man på hvad værdien er ved henholdsvis 25%, 50% og 75%. Kigger vi på tabellen med biler ovenfor kan vi se at:

$ Q_1 $ = 1. kvartil (25%) = 0 biler
$ Q_2 $ = 2. kvartil (50%) = 1 bil
$ Q_3 $ = 3. kvartil (75%) = 1 bil

Variationsbredde

Variationsbredden beskriver forskellen mellem mindste og største værdien. Det kan give en indikation af hvor bredt man har ramt med sin undersøgelse. Tallet findes ved beregning:

Forstil dig eksemplet med bilerne ovenfor. Hvis vores undersøgelse havde vist at der var en person med 20 biler, så ville variationsbredden have været $ 20-0 = 20 $. Hvis man sammenholder den med kvartilsættet, så bliver det tydeligt at se at det på ingen måde er normen.

Varians

Varians er en matematisk størrelse der anvendes til at beskrive hvordan data fordeler sig og anvendes i forskellige sammenhænge når man regner med statistik. Variansen angives med $ Var(x) $.

Variansen kan altså beskrive hvordan observationerne er fordel. Er tallet lavt ligger observationerne tæt. Er tallet højt ligger det spredt.

Man skal dog være bevidst om at variansen skal beregnes på forskellige måder afhængigt af om ens datamateriale er skabt af en population eller en stikprøve. Ved en population angiver man variansen med $ \sigma^2 $ og ved en stikprøve som $ s^2 $.

I praksis anvender man altid stikprøveformlen. Det skyldes at man sjældent har et komplet datasæt.

Populationsformlen

$$ \sigma^2 = \sum_{i=1}^k (x_i- \overline x)^2 \cdot f_i ~~~~= ~~~~ \frac{1}{n} \cdot \sum_{i=1}^k (x_i- \overline x)^2 \cdot h_i$$

Stikprøveformlen

$$ s^2 = \frac{1}{n-1} \cdot \sum_{i=1}^k (x_i- \overline x)^2 \cdot h_i$$

Årsagen til $ \frac{1}{n-1} $ er, at man under beregningen af middelværdien ($ \overline x $) allerede har anvendt alle værdierne i datamaterialet. Man kan sige at hvis man ikke kompenserer for dette, så er variansen påvirket (biased) pga. dette. Sagt på en anden måde: Hvis man ved at gennemsnittet af $ 3 $ tal er $ 6 $, og to af tallene er $ 5 $ og $ 6 $, så skal det sidste tal være $ 7 $. Der er altså reelt kun $ n-1 $ grader af frihed.

Læs mere: http://duramecho.com/Misc/WhyMinusOneInSd.html

Forklaring på formlen

$ x_i- \overline x $

Beskriver differencen mellem den enkelte observartion og gennemsnittet

$ (x_i- \overline x)^2 $

For at gøre differencen positiv og sikre sig at store differencer også påvirker resultatet mere

$ h_i $

For at finde finde ud af hvor ofte differencen forekommer

$ \sum_{i=1}^k $

Gøres for hver enkelt observation

$ \frac{1}{n-1} $

Det samlede tal for differencen spredes ud over alle observationerne. $ \frac{ 1 }{ n-1 } $ fordi det er en stikprøve.

$ s^2 $

Når vi har kvadreret på den ene side skal vi også gøre det på den anden.

Regnearksformler

Statistisk funktion	Beskrivelse
varians.s(Område)	variansen for en stikprøve
varians.p(Område)	variansen for en population
stdafv.s(område)	Standardafvigelsen/spredningen for en stikprøve
stdafv.p(område)	Standardafvigelsen/spredningen for en population

Spredning/standardafvigelse

Spredningen fortæller noget om fordelingen af værdier i forhold til gennemsnittet og er kvadratroden af variansen. Generelt kan spredningen altså skrives som $ \sqrt{Var(x)} $.

For populationer: $ \sigma = \sqrt{\sigma^2} $

For stikprøver: $ s = \sqrt{s^2} $

Spredningen/standardafvigelsen kan altså beskrive hvordan observationerne er fordel. Er tallet lavt ligger observationerne tæt. Er tallet højt ligger det spredt.

Normalfordeling/normaldistribution

Indenfor statistik anvender man begrebet normalfordeling, når data fordeler i det man kalder en "bell-curve". Årsagen til at man anvender "normal" er fordi man ofte ser den når man arbejder med statistisk materiale.

https://commons.wikimedia.org/wiki/File:Normal_Distribution_PDF.svg

Diagrammer

For at skabe et hurtig overblik over sin undersøgelse kan man lave diagrammer. De to mest anvendelige i denne sammenhæng er søjle- og lagkagediagrammet

Søjlediagram

Cirkeldiagram

Notation

Når man beregner Statisk meteriale anvender man følgende notation.

Symbol	Forklaring
$ n $	Antallet af observationer
$ k $	Antal observationssæt/værdier
$ \overline x $	Gennemsnitsværdien af $ x $
$ m $	Interval midtpunkt. Den midterste værdi i et interval f.eks. $ ]160;170] = \frac{161+170}{2} = 165.5 $
$ \sigma^2 $/$ s^2 $	Variansen. $ \sigma^2 $ anvendes når det er en population og $ s^2 $ når det er en stikprøve.
$ \sigma $/$ s $	Spredningen.$ \sigma $ anvendes når det er en population og $ s $ når det er en stikprøve.
$ \sum $	Summen af .... .Dette er det store bogstav sigma fra det græske alfabet

Varians og spredning fortæller noget om hvor stor spredningen er i datasættet. Altså om observationerne ligger kort eller langt fra middelværdien.

Beregninger - diskret fordeling

Datasæt i en tabel

For at få et overlbik over vores data indsætter man dem i en tabel som herunder:

Tabel: Karakterer
$ x_i $	$ x $	$ h(x) $	$ f(x) $
$ x_1 $	$ 02 $	$ 1 $	$ 0,1 $
$ x_2 $	$ 4 $	$ 2 $	$ 0,2 $
$ x_3 $	$ 7 $	$ 4 $	$ 0,4 $
$ x_4 $	$ 10 $	$ 2 $	$ 0,2 $
$ x_5 (x_k) $	$ 12 $	$ 1 $	$ 0,1 $

Antal observationer

Antallet af observationer kan ved små datasæt tælles, men hvis datasættet er stort anvender man følgende formel, hvor $ k $ er antallet af observationsværdier:

$$ n = \sum_{i=1}^{k} h_i $$

Beregning af $ n $

$$ n = \sum_{i=1}^{k} h_i ~~\Rightarrow~~ n = \sum_{i=1}^{5} h_i = 1+2+4+2+1 = 10$$

Middelværdi (gennemsnit)

Gennemsnittet kan beregnes med 2 formler alt efter om man anvender frekvens:

$$ \overline x = \sum_{i=1}^{k} x_i \cdot f_i $$

... eller hyppighed da $ f_i = \frac{1}{n} \cdot h_i $:

$$ \overline x = \frac{1}{n} \cdot \sum_{i=1}^{k} x_i \cdot h_i $$

Beregnet med frekvens:

$$ \overline x = \sum_{i=1}^{5} x_i \cdot f_i= (0,1 \cdot 2 + 0,2 \cdot 4 + 0,4 \cdot 7 + 0,2 \cdot 10 + 0,1 \cdot 12) = 7$$

Beregnet med hyppighed:

$$ \overline x = \frac{ 1}{10} \cdot \sum_{i=1}^{5} x_i \cdot h_i= \frac{1}{10} \cdot (2 \cdot 1 + 4 \cdot 2 + 7 \cdot 4 + 10 \cdot 2 + 12 \cdot 1) = \frac{1}{10} \cdot 70 = 7$$

Varians

For en stikprøve er formlen:

$$ s^2 = \frac{1}{n-1} \cdot \sum_{i=1}^k (x_i- \overline x)^2 \cdot h_i$$

Anvendt på tabellen, som er en stikprøve:

$$ s^2 = \frac{1}{10-1} \cdot \sum_{i=1}^5 (x_i- 7)^2 \cdot h_i \\ \Updownarrow \\ s^2 = \frac{1}{9} \cdot \left((02-7)^2 \cdot 1 + (4-7)^2 \cdot 2 + (7-7)^2 \cdot 4 + (10-7)^2 \cdot 2 + (12-7)^2 \cdot 1 \right) \\ \Updownarrow \\ s^2 = \frac{1}{9} \cdot \left( (-5)^2 \cdot 1 + (-3)^2 \cdot 2 + 0^2 \cdot 4 + 3^2 \cdot 2 + 5^2 \cdot 1 \right) \\ \Updownarrow \\ s^2 = \frac{1}{9} \cdot (25+18+0+18+25) \\ \Updownarrow \\ s^2 = 9,556 $$

Spredning/standardafvigelse

Spredningen er kvadratroden af variansen hvilket vil sige:

For en population:

$$ \sigma = \sqrt {s^2} $$

For en stikprøve:

$$ s = \sqrt {s^2} $$

Spredningen er altså:

$$ s = \sqrt {s^2} = \sqrt {9,556} = 3,091 $$

Beregninger - kontinuert data

Et datasæt

Herunder er en tabel over højden på 20 volleyballspillere.

Observation $ x_i $	Højde $ ]x_{i-1};x_i] $	Antal $ h(x) $	Frekvens $ f(x) $	Interval midtpunkt $ m(x) $
$ x_1 $	$ ]160;170] $	$ 3 $	$ 0,15 $	$ 165 $
$ x_2 $	$ ]170;180] $	$ 9 $	$ 0,45 $	$ 175$
$ x_3 $	$ ]180;190] $	$ 3 $	$ 0,15 $	$ 185 $
$ x_4 $	$ ]190;200] $	$ 4 $	$ 0,2 $	$ 195 $
$ x_5 $	$ ]200;210] $	$ 1 $	$ 0,05 $	$ 205 $

Antal observationer

Udregnes som ved diskret fordeling

$$ n = \sum_{i=1}^{k} h_i $$

Dvs

$$ n = \sum_{i=1}^{k} h_i \Rightarrow n = \sum_{i=1}^{5} h_i = 3+9+3+4+1 = 20$$

Interval Midtpunkt

Interval midtpunktet findes ved at tage halvdelen af summen af mindsteværdien ($ x_i $) og størsteværdien i intervallet ($ x_{i+1} $):

$$ m_i = \frac{1}{2} \cdot (x_{i} + x_{i+1})$$

F.eks. af intervallet $ ]180:190] $

$$ m_i = \frac{1}{2} \cdot (180 + 190) = 185$$

Middelværdi (gennemsnit)

Gennemsnittet kan beregnes med 2 formler alt efter om man anvender frekvens:

$$ \overline x = \sum_{i=1}^{k} m_i \cdot f_i $$

... eller hyppighed da $ f_i = \frac{1}{n} \cdot h_i $:

$$ \overline x = \frac{1}{n} \cdot \sum_{i=1}^{k} m_i \cdot h_i $$

Middeltal beregnet med frekvens:

$$ \overline x = \sum_{i=1}^{5} m_i \cdot f_i = 165 \cdot 0,15 + 175 \cdot 0,45 + 185 \cdot 0,15 +195 \cdot 0,2 + 205 \cdot 0,05 = 180,50 $$

Middeltal beregnet med hyppighed:

$$ \overline x = \frac{1}{20} \cdot \sum_{i=1}^{5} m_i \cdot h_i = \frac{1}{20} \cdot \left(165 \cdot 3 + 175 \cdot 9 + 185 \cdot 3 +195 \cdot 4 + 205 \cdot 1 \right) = 180,50$$

Varians

Variansen beskriver hvor meget værdierne i gennemsnit afviger fra middelværdien. Når man angiver variansen skal man først forholde sig til om det er for en population eller en stikprøve.

Er det fra en population kaldes variansen for $ \sigma^2 $ og er det fra en stikprøve kaldes den for $ s^2 $.

For en population er formlen:

$$ \sigma^2 = \sum_{i=1}^k (m_i- \overline x)^2 \cdot f_i$$

2) ( da: $ f_i = \frac{1}{n} \cdot h_i $ )

$$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^k (m_i- \overline x)^2 \cdot h_i$$

For en stikprøve

$$ s^2 = \frac{1}{n-1} \cdot \sum_{i=1}^k (m_i- \overline x)^2 \cdot h_i$$

Anvendt på tabellen, som er en stikprøve:

$$ s^2 = \frac{1}{20-1} \cdot \sum_{i=1}^5 (m_i- 180,5)^2 \cdot h_i \\ \Updownarrow \\ s^2 = \frac{1}{19} \cdot \left( (165-180,5)^2 \cdot 3 + (175-180,5)^2 \cdot 9 + (185-180,5)^2 \cdot 3 + \\(195-180,5)^2 \cdot 4 + (205-180,5)^2 \cdot 1 \right) \\ \Updownarrow \\ s^2 = \frac{1}{19} \cdot \left( (-15,5)^2 \cdot 3 + (-5,5)^2 \cdot 9 + (4,5)^2 \cdot 3 + (14,5)^2 \cdot 4 + (25,5)^2 \cdot 1 \right) \\ \Updownarrow \\ s^2 = \frac{1}{19} \cdot \left( 240,25 \cdot 3 + 30,25 \cdot 9 + 20,25 \cdot 3 + 210,25 \cdot 4 + 650,25 \cdot 1 \right) \\ \Updownarrow \\ s^2 = 133,95 $$

Spredning

Spredningen er kvadratroden af variansen hvilket vil sige:

For en population:

$$ \sigma = \sqrt {\sigma^2} $$

For en stikprøve:

$$ s = \sqrt {s^2} $$

Spredningen er altså:

$$ s = \sqrt {133.95} = 11,57 $$

Regneark

Herunder er de forskellige funktioner fra regneark angivet.

Når der henvises til Område, så er det datasættet der skal indsættes.

Statistisk funktion	Beskrivelse
tæl(Område)	Antal observationer (værdier)
tælv(Område)	Antal observationer (ikke tomme felter)
tæl.hvis(Område;Betingelse)	Antal observationer i området der opfylder betingelsen. Hvis betingelsen er et tegn skal det omgives med anførselstegn (f.eks: ") .
middel(Område)	Gennemsnit
min(Område)	Mindste værdi
maks(Område)	Største værdi
hyppigst(Område)	hyppigste værdi
median(Område)	Medianen
kvartil(Område;1/2/3)	Første, anden og tredje kvartil

Angående kvartilsæt

Når regneark finder 1. og 3. kvartil anvender de en anden metode, end den man "normalt" anvender. Det er en vægtet kvartil, så derfor kan det godt være et tal der ikke optræder i selve tabellen.

Varians og standardafvigelse

Excel/Calc	Sheets	Beskrivelse
varians.s(Område)	_	variansen for en stikprøve
varians.p(Område)	_	variansen for en population
stdafv.s(område)	_	Standardafvigelsen/spredningen for en stikprøve
stdafv.p(område)	_	Standardafvigelsen/spredningen for en population

Tilfædige tal

Excel/Calc	Sheets*	Beskrivelse
SLUMP()	RAND()	Laver et tilfældigt tal i intervallet [0;1]
SLUMPMELLEM(start;slut)	RANDBETWEEN(start;slut)	Returnerer den positive værdi af et tal

Likert skalaen

Nogle gange har man brug for at finde ud af i hvilken grad man vurderer et spørgsmål positivt eller negativt. Det kan gøres med en Likert skala. Den store danske beskriver en Likert skala på følgende måde:

Likert-skala, sociologisk skala til måling af holdninger, udviklet af den amerikanske socialpsykolog Rensis Likert (1903-81). Forsøgspersoners grader af samtykke/modvilje i forhold til en række påstande gives hver en værdi, som summeret udtrykker en holdnings styrke.

Herunder er vist 3 eksempler på Likertskalaen. Det man skal overveje når man anvender denne skala er, flere ting:

Hvor nuanceret skal resultatet være
Hvor nøjagtig kan (vil?) respondenten svare
Hvor langt tid skal/kan respondenten anvende til hvert svar

Det man altså skal finde ud af er, hvor store nuancer man få sat op imod det som respondenten vil kunne svare på. Er skalaen for stor risikerer man at få svar der ikke er nøjagtige.

Likert skala 5 trin

Negativ		Neutral		Positiv
1	2	3	4	5

Likert skala 7 trin

Negativ			Neutral			Positiv
1	2	3	4	5	6	7

Likert skala 9 trin

Negativ				Neutral				Positiv
1	2	3	4	5	6	7	8	9

Et eksempel

Kantinen har eksperimenteret med en ny ret og har spurgt hvad folk syntes om maden. Til dette har de anvendt en 7 trins likert skala, hvor 7 er det bedste og 1 er dårligst. Tallene fordeler sig på følgende måde:

Vurdering ($ x_i $)	1	2	3	4	5	6	7
Antal ($ h(x_i) $)	2	8	2	4	4	3	1

Ved beregning finder vi:

Antal observationer = 24
Middelværdi = 3,542
Mindste værdi = 1
Højeste værdi = 7
Hyppigste værdi = 2
Median = 3,5
$ Q_1 $ = 2
$ Q_2 $ = 4
$ Q_3 $ = 5
Varians = 2,998
Spredning/standardafvigelse = 1,732

En hurtig tolkning vil altså være at den nye ret ikke har været populær, da middelværdien ligger under neutralt. Der er også mange der decideret ikke har brudt sig om maden (hyppigste værdi). Derudover er det en ret stor varians og spredning, som indikerer at retten skaber mange meninger.

Konklusion - der skal findes en anden ret, da denne ret nok kommer til at kæmpe mod et dårligt ry, og der mangler en gruppe af mennesker der er begejstret for den.

regneark_statistik_likert.xls

Antal biler (\( x \))	\( h(x) \)	\( H(x) \)	\( f(x) \)	\( F(x) \)
\( 0 \)	\( 40 \)	\( 40 \)	\( 0,40 \)	\( 0,40 \)
\( 1 \)	\( 44 \)	\( 84 \)	\( 0,44 \)	\( 0,84 \)
\( 2 \)	\( 14 \)	\( 98 \)	\( 0,14 \)	\( 0,98 \)
\( 3+ \)	\( 2 \)	\( 100 \)	\( 0,02 \)	\( 1,00 \)

Antal biler (\( x \))	\( h(x) \)	\( H(x) \)	\( f(x) ~/~ P(X=x)\)	\( F(x) ~/~ P(X \leq x)\)
\( 0 \)	\( 40 \)	\( 40 \)	\( 0,40 \)	\( 0,40 \)
\( 1 \)	\( 44 \)	\( 84 \)	\( 0,44 \)	\( 0,84 \)
\( 2 \)	\( 14 \)	\( 98 \)	\( 0,14 \)	\( 0,98 \)
\( 3+ \)	\( 2 \)	\( 100 \)	\( 0,02 \)	\( 1,00 \)

Symbol	Forklaring
\( n \)	Antallet af observationer
\( k \)	Antal observationssæt/værdier
\( \overline x \)	Gennemsnitsværdien af \( x \)
\( m \)	Interval midtpunkt. Den midterste værdi i et interval f.eks. \( ]160;170] = \frac{161+170}{2} = 165.5 \)
\( \sigma^2 \)/\( s^2 \)	Variansen. \( \sigma^2 \) anvendes når det er en population og \( s^2 \) når det er en stikprøve.
\( \sigma \)/\( s \)	Spredningen.\( \sigma \) anvendes når det er en population og \( s \) når det er en stikprøve.
\( \sum \)	Summen af .... .Dette er det store bogstav sigma fra det græske alfabet

Tabel: Karakterer
\( x_i \)	\( x \)	\( h(x) \)	\( f(x) \)
\( x_1 \)	\( 02 \)	\( 1 \)	\( 0,1 \)
\( x_2 \)	\( 4 \)	\( 2 \)	\( 0,2 \)
\( x_3 \)	\( 7 \)	\( 4 \)	\( 0,4 \)
\( x_4 \)	\( 10 \)	\( 2 \)	\( 0,2 \)
\( x_5 (x_k) \)	\( 12 \)	\( 1 \)	\( 0,1 \)

Observation \( x_i \)	Højde \( ]x_{i-1};x_i] \)	Antal \( h(x) \)	Frekvens \( f(x) \)	Interval midtpunkt \( m(x) \)
\( x_1 \)	\( ]160;170] \)	\( 3 \)	\( 0,15 \)	\( 165 \)
\( x_2 \)	\( ]170;180] \)	\( 9 \)	\( 0,45 \)	\( 175\)
\( x_3 \)	\( ]180;190] \)	\( 3 \)	\( 0,15 \)	\( 185 \)
\( x_4 \)	\( ]190;200] \)	\( 4 \)	\( 0,2 \)	\( 195 \)
\( x_5 \)	\( ]200;210] \)	\( 1 \)	\( 0,05 \)	\( 205 \)