Formelsamling
Regneregler
Man siger at \( + \) og \( \cdot \) er kommunikative da rækkefølgen er uden betydning.
Man kan omskrive negative tal og brøker, så man kan arbejde kommunikativt med dem.
Matematiske sætninger
For at kunne snakke om matematik anvender vi et fagsprog, hvor vi anvender begreber som led og sætning. En matematisk sætning er opbygget af led, som er adskilt af \( + \) eller \( - \). Lad os kigge på nedestående matematiske udtryk, der består af 3 led:
Positive led kan flyttes rundt efter behov, så det kræver en omskrivning af de negative led, for at kunne flytte dem på samme måde.
Brøkregneregler
Brøker tilhører talmængden \( \mathbb{Q} \). For at kunne beskrive brøker anvender vi begreberne tæller og nævner:
Addition og substraktion
For at kunne lægge brøker sammen skal de have samme nævner
Multiplikation
Division
Når man dividerer med en brøk så ganger man med den reciprokke (modsatte) værdi
Eksempler med brøker
Addition
Substraktion
Multiplikation
Division
Faktorering
Tal der ganges med hinanden kaldes faktorer.
I matematik kan man have fordel af at faktorere tal ved hjælp af primtalsfaktorer. Primtal er tal, hvor kun en og tallet selv går op i tallet. Herunder er de første 17 primtal:
Se nedestående eksempel:
Det kan f.eks. anvendes til at forkorte brøker.
Numeriske værdier
For at sikre et tal kommer ud som en positiv værdi anvender man nummeriske værdier:
Kvadratsætningerne
Sætning 1:
Når det er en plus parentes er det:
- Det første led i anden plus det andet led i anden
- plus
- det dobbelte produkt af ledene
Sætning 2:
Når det er en minus parentes er det:
- Det første led i anden plus det andet led i anden
- minus
- det dobbelte produkt af ledene
Sætning 3:
Når det er en plus og en minus parentes er det:
- Det første led i anden minus det andet led i anden
Eksempler med kvadratsætninger
Plus parantes
\( (2x+4)^2 = (2x)^2 + (4)^2 + 2 \cdot (2x \cdot 4) = 4x^2 + 16 + 16x\)
Minus parantes
\( (2x-4)^2 = (2x)^2 + (4)^2 - 2 \cdot (2x \cdot 4) = 4x^2 + 16 - 16x \)
Plus og minus parantes
\( (2x+4) \cdot (2x-4) = (2x)^2 - (4)^2 = 4x^2 - 16 \)
Potensregler
Definitioner
Definition 1
Definition 2
Definition 3
Definition 4
Benævnelser
Benævnelsen for tallene \( a^x = y \) er:
- \( a \) = rodtallet (basen)
- \( x \) = exponenten
- \( y \) = potensen
Regneregler
Eksempler med potensregneregler
Regneregel 1
\( 2^3 \cdot 2^4 = 2^{3+4} = 2^7 \)
Regneregel 2
\( (2^3)^4 = 2^{3 \cdot 4} = 2^{12} \)
Regneregel 3
\( (2 \cdot 3)^4 = 2^4 \cdot 3^4 ← regneregel 1 \)
Regneregel 4
\( \frac{ 2^3 }{ 2^4 } = 2^{3-4} = 2^{-1} \)
Regneregel 5
\( \frac{ 2^4 }{ 3^4 } = \left( \frac{ 2 }{ 3 }\right)^4 \)
Regneregel 6
\( \sqrt[3]{2} = 2^{\frac{ 1 }{ 3 }} \)
Regneregel 7
\( \sqrt[3]{2^4} = 2^{\frac{ 4 }{ 3 }} \)
Logaritmer
Definitioner
Logaritmefunktionen \( log_a(x) \) er defineret på følgende måde, hvor \( a \) er grundtallet:
Definition 1
Definition 2
Definition 3
Definition 4
Den naturlige logaritme
Indenfor matematik anvender man ofte den naturlige logaritme hvor grundtallet er \( e \approx 2,718281828 \). Den kaldes også for ln, hvor det gælder at \( ln(e) = 1 \)
Formlerne herunde er lavet med ln
Regneregler (omskrivninger)
De generelle regnereglerne for logaritmer er:
Ved alle de nedestående formler kan \( ln \) erstattes med \( log \).
Eksempler med logaritmer (omskrivninger)
Regneregel 1
\( ln(3 \cdot 7) = ln(3) + ln(7) \)
Regneregel 2
\( ln(\frac{3}{7}) = ln(3) - ln(7) \)
Regneregel 3
\( ln(3^7) = 7 \cdot ln(3) \)
Ligningsløsning
Når man løser ligninger bruger man følgende fremgangsmåde
- Reducer utrykket og sæt udenfor parantes (hvis det er smart)
- Isoler den ubekendte
Når man isolerer den ubekendte gælder der den regel, at der skal være "ligevægt" i ligningen. Det betyder at man skal gøre det samme på begge sider, f.eks:
Først trækker vi \( 7 \) fra på begge sider:
Herefter dividerer vi med \( 4 \) på begge sider:
Her bliver det meget pindet ud, men man bør skrive det uden melemregningere, når det er simpel hovedregning (her noteret lodret:
Når man løser ligninger anvender man tegnene:
- ensbetydende: \( \Leftrightarrow ~~ \Updownarrow \) (biimplikation)
- medfører: \( \Rightarrow ~~ \Downarrow \) implikation
Forskellen mellem dem er følgende
Ensbetydende (bimplikation)
Man bruger enbestydende når udtrykkene på hver side
Lad os kigge på følgende eksempel på en ligningsløsning
Her anvende vi ensbetydende, fordi de efterfølgende udtryk alle kommer fra det første. Det betyder også at vi kan sige nedestående fordi de kan afledes af hinanden:
Sagt på en anden måde ... uanset om vi tager udtrykket til venstre eller til højre, så kan vi føre dem hen til det andet.
Medfører (implikation)
Nogle gange kan vi ikke gå begge veje. Det gælder f.eks. i følgende tilfælde:
Det er korrekt, at \( 3^2 = 9 \), men \( \sqrt{9} \) kan være både \( 3 \) og \( -3 \).
Skema
Hovedregel: Man skal gøre det samme på begge sider
| Hvad skal fjernes/tilføjes | Løsning |
|---|---|
| Led | lægge til / trække fra |
| Faktorer | gange / dividere |
| Eksponenter | Logaritmer |
| Potenser | rødder |
| Parenteser | samler led |
| Ændre fortegn | gange med \( -1 \) |
Praktiske eksempler
Leda)
b)
a)
b)
Mængdelære
Lad os antage at vi har mængerne:
Foreningsmængde
Venn-diagram
Fællesmængde
Venn-diagram
Symetrisk differens
Venn-diagram
Mængdedifferens
Venn-diagram
Komplementærmængde
Tal der ikke findes i mængden.
Venn-diagram
Talmængder
Hele tal
\( \mathbb{N} = \{1, 2, 3 ...\} \)
\( \mathbb{N_0} = \{0, 1, 2, 3 ...\} \)
\( \mathbb{Z} = \{...-2, -1, 0, 1, 2...\} \)
Rationelle og reelle tal
Rationel betyder: "styret af eller baseret på fornuft, logik og materiel virkelighed" (DDO). Kort fortalt - brøker.
Der findes dog nogle tal som ikke kan skrives som brøker f.eks.: \( \pi \) og \( \sqrt{2} \). Da de tal ikke kan skrive som brøker kalder man dem irrationelle tal - altså tal der ikke er styret af "fornuft, logik og materiel virkelighed". I daglig tale kaldes disse for de reelle tal.
Rationelle tal\( \mathbb{Q} = \ \left\{ \frac{ a }{ b } ~\middle| ~a,b \in \mathbb{Z} \wedge b \neq 0\right\} \)
Den ovenstående matematisk sætning læses som følger:
"Talmængden \( \mathbb{Q} \) er brøker (\( \frac{ a }{ b } \)), hvorom det gælder (\( \left. \right| \)), at a og b (\( a,b \)) tilhører (\( \in \)) talmængden \( \mathbb{Z} \), og at b skal være forskelligt fra 0 (\( b \neq 0 \))"
Irationelle talDe tal som ikke er repræsenteret af \( \mathbb{N},\mathbb{N_0}, \mathbb{Z} \) og \( \mathbb{Q} \) kaldes for de irationelle tal. Talmængden har ikke sit eget symbol, men kan skrives som \( \mathbb{R} \)\\( \mathbb{Q} \). Det læses som alle elementer i de relle tal uden elementerne i de rationelle tal.
Reelle talDe reelle tal er alle de tal der reelt findes. Dvs. alle de ovenstående talmængder og de irrationelle tal. De reelle tal angives med symbolet \( \mathbb{R} \)
Komplekse tal
Der findes dog endnu en talmængde nemlig de komplekse tal, som er opbygget af en reel og en imaginær del. Imaginær betyder "Findes kun i eller udspringer af en persons fantasi" (DDO ). Den imaginære del er tallet, hvorom det gælder at \( i^2 = -1 \). Denne talmængde skrives med \( \mathbb{C} \)
Intervaller
Her er nogle eksempler på intervaller.
\( [ ~a~;~ b ~] \) eller \( a \leq x \leq b \)
\( ] ~a~; ~b~ ] \) eller \( a < x \leq b \)
\( ] ~a~; ~b~ [ \) eller \( a < x < b \)
\( ] ~-\infty~ ; ~a~ ] \) eller \( x \leq a \)
Funktionsbegrebet
En funktion er defineret ved at der til hvert \( x \) tilhører et, og kun et \( y \).
Koordinatsystemet
Funktionsværdi
Funktionsværdien, \( f(x) = y \), er den værdi funktionen antager, når man anvender \( x \) i funktionen.
Definitionsmængden (Dm)
Definitionsmængden beskriver de værdier på x-aksen, hvor funktionen er gyldig. Her:
\( Dm(f) = ] ~a~;~d~ ] \) eller \( Dm(f) = a < x \leq d \)
Værdimængden (Vm)
Værdimængden beskriver de værdier på y-aksen, som funktionen kan antage. Her:
\( Vm(f) = [ ~e~;~g~] \) eller \( Vm(f) = e \leq y \leq g \)
Ekstrema
Ekstrama angiver de steder hvor funktionen har sine højeste og laveste værdier. Den højeste værdi kalder for maximum den laveste for minimum. Er der flere kaldes de for ekstrema
Den ovenstående funktion har ekstrema i x-værdierne \( b \) og \( c \)
- Højeste værdi i \( b \)
- Laveste værdi i \( c \)
Når en funktion har en absolut mindste eller største værdi (f.eks. en parabel), taler man om et "globalt ekstrema"
Monotoniforhold
For funktionen \( f \) gælder følgende monotoniforhold
- \( f \) er aftagende/faldende for \( ]~a~;~e~] \).
- \( f \) er tiltagende/voksende for \( [~e~;~c~] \).
- \( f \) er aftagende/faldende for \( [~c~;~d~] \).
Funktionsanalyse
Når man laver en funktionsanalyse beskriver man en funktion ud fra 6 punkter:
- En graf af funktionen
- Definitionsmængde (Dm)
- Værdimængde (Vm)
- Nulpunkter og fortegn
- \( f(x) = 0 \)
- \( f(x) > 0 \)
- \( f(x) < 0 \)
- Monotoniforhold
- Ekstrema
Tegn grafen i en graftegner så du kan se funktionen med du arbejder med den.
Hvilke x-værdier kan anvendes
Hvilke y-værdier kan funktionen have
Det man undersøger er, hvornår:
Hvor er funktionen stigende og faldende
Hvor har funktionen sin største eller mindste værdi. Hvis en funktion har flere "toppe" eller "dale" kan man beskrive lokale ekstrema
Funktioner
Linjen
Lineære funktioners normalform er:
Man kan finde ligningen til den lineære funktionen ved hjælp af to punkter på linjen.
Formlerne for \( a \) og \( b \)
Eksponentielle funktioner
Eksponentialfunktioner normalform er:
\( a \) kaldes for fremskrivningsfaktoren og \( b \) for begyndelsesværdien.
Man kan finde ligningen til eksponentialfunktionen ved hjælp af to punkter.
Formlerne for \( a \) og \( b \)
Formlerne for fordoblingskonstanten (\( T_2 \)) og halveringskonstanten (\( T_{\frac{1}{2}} \)) er
Potensfunktioner
Potensfunktionens normalform er:
Man kan finde ligningen til eksponentialfunktionen ved hjælp af to punkter.
Formlerne for \( a \) og \( b \)
Andengradsligningen
Andengradsligningens normalform er:
For at løse andengradsliningen anvendes følgende formel
Toppunkt
For at finde parablens toppunkt anvendes følgende formel
Antal rødder
Diskriminanten (\( D \)) beskriver antallet af rødder andengradsligning har.
Gaflernes orrientering
Fortegnet for \( a \) angiver gaflernes orrientering. Hvis \( a \) er positiv vender parablens gafler opad og hvis \( D \) er negativ vender de nedad.
Konstruktion af andegradsligninger
Man kan konstruere andengradsligninger med følgende formel:
Statistik
Begreber
Observation, hændelse og udfald
Observation: Noget man aktivt observerer.
Hændelse: Noget som sker f.eks. et biluheld.
Udfald: Noget der sker pga. en sandsynlighed f.eks. terningkast.
Population og stikprøve
En population er et datasæt der indeholder alle data... Har man ikke alle data taler man om stikprøve.
Repræsentativt datasæt
Et datasæt (stikprøve) der har data nok til at lave en nøjagtig beskrivelse af populationen.
Diskret og kontinuert data
Diskret data er eksakte værdier, hvor kontinuert data er grupperede værdier.
Symboler
| Symbol | Begreb | Definition | Talmængde |
|---|---|---|---|
| \( x \) | Observation | Anvendt data | |
| \( h(x) \) | Hyppighed | Hvor ofte en observation/hændelse optræder | \( \mathbb{N}_0 \) |
| \( H(x) \) | Summeret hyppighed | Hvor ofte denne og forgående observationer/hændelser optræder | \( \mathbb{N}_0 \) |
| \( f(x) \) | Frekenvens | Hvor ofte en observation/hændelse optræder i forhold til det samlede antal observationer | \( \mathbb{R} \) |
| \( F(x) \) | Summeret frekenvens | Hvor ofte denne og forgående observationer/hændelser optræder i forhold til det samlede antal observationer | \( \mathbb{R} \) |
Deskriptorer
| Deskriptor | Forklaring | Metode |
|---|---|---|
| Typetal (diskret data) | Den obeservation der forekommer flest gange | Aflæsning |
| Typeinterval (kontinuert data) | Den samling af observationer der er flest af | Aflæsning |
| Mindste værdi | Den mindst observerede værdi | Aflæsning |
| Største værdi | Den størst observerede værdi | Aflæsning |
| Median | Den midterste observation. Er det samme som 50% kvartilen (se nedenfor) | Aflæsning |
| Middelværdi | Gennemsnit | Beregning |
Notation
| Notation | Forklaring |
|---|---|
| \( n \) | Antallet af observationer |
| \( k \) | Antal observationssæt/værdier |
| \( \overline x \) | Gennemsnitsværdien af \( x \) |
| \( m \) | Interval midtpunkt. Den midterste værdi i et interval f.eks. \( ]160;170] = \frac{161+170}{2} = 165.5 \) |
| \( \sigma^2 \)/\( s^2 \) | Variansen. \( \sigma^2 \) anvendes når det er en population og \( s^2 \) når det er en stikprøve. |
| \( \sigma \)/\( s \) | Spredningen.\( \sigma \) anvendes når det er en population og \( s \) når det er en stikprøve. |
| \( \sum \) | Summen af .... .Dette er det store bogstav sigma fra det græske alfabet |
\( \sum \) - opsummer
Lad os kigge på et simpelt datasæt over karakterer. For at danne os et overblik over tabellen vælger vi at lave to rækker (\( x \) og \( x_i \)). En hvor tallene står og en hvor vi angiver positionerne ved hjælp af værdierne \( x_1 \) til \( x_k \), hvor \( k \) er den sidste observation.
| Generelt datasæt | ||||||
|---|---|---|---|---|---|---|
| \( x_i \) | \( x_1 \) | \( x_2 \) | \( x_3 \) | \( ... \) | \( x_{k-1} \) | \( x_k\) |
Hvis vi ville opsummere tallene ville vi altså lave regnestykket: \( x_1+x_2+x_3+...+x_{k-1}+{x_k} \)
Dette kan skrives som:
Udtrykket læses på denne måde: Opsummer \( x_i \), mens i gennemløber værdierne fra \( i=i \rightarrow k\).
\( \sum \) anvendes som ethvert andet tegn i matematikken f.eks:
Diagrammer
For at skabe et hurtig overblik over sin undersøgelse kan man lave diagrammer. De to mest anvendelige i denne sammenhæng er søjle- og lagkagediagrammet
Søjlediagram
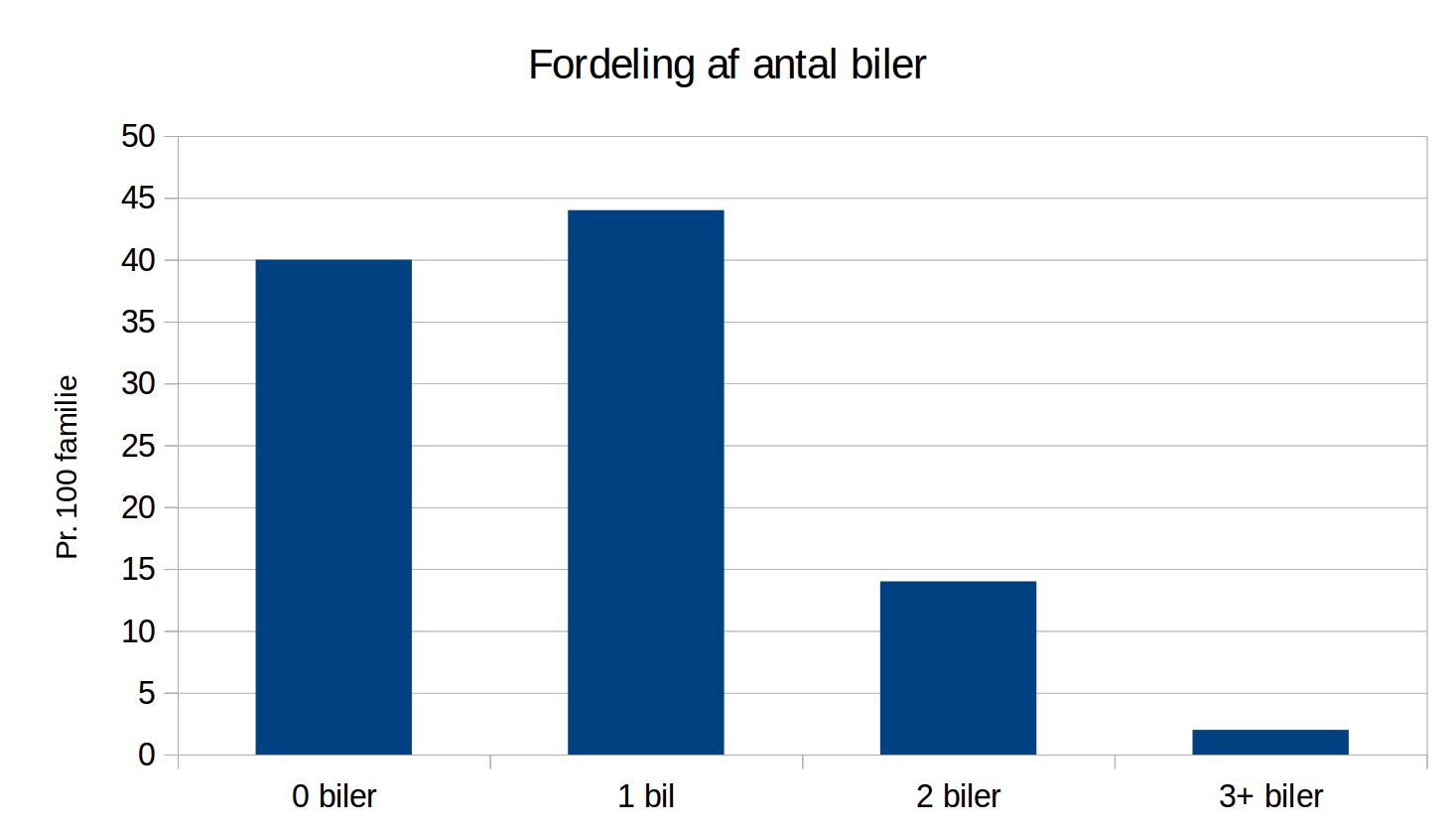
Cirkeldiagram
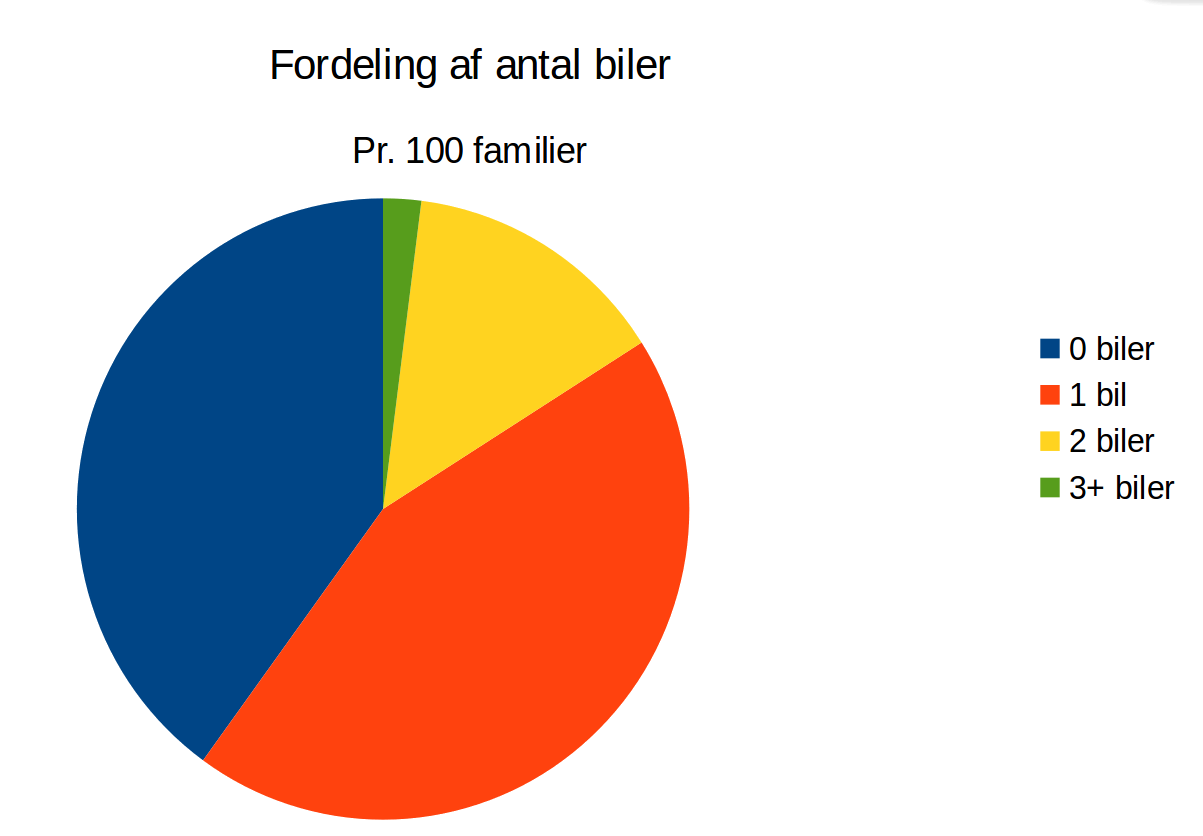
Diskret fordeling
Eksempel på tabel
Denne tabel indeholder karakterfordelingen for 10 elever.
| Tabel 2 (Kontinuerte observationer): Karakterer | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| x | \( h(x) \) | \( f(x) \) | |||||||
| \( 02 \) | \( 1 \) | \( 0,1 \) | |||||||
| \( 4 \) | \( 2 \) | \( 0,2 \) | |||||||
| \( 7 \) | \( 4 \) | \( 0,4 \) | |||||||
| \( 10 \) | \( 2 \) | \( 0,2 \) | |||||||
| \( 12 \) | \( 1 \) | \( 0,1 \) | |||||||
Antal observationer
Middelværdi (gennemsnit)
1)
2)
Varians
For en population:
1)
2) ( da: \( f_i = \frac{1}{n} \cdot h_i \) )
For en stikprøve
Spredning/standardafvigelse
For en population:
For en stikprøve
Kontinuert data
Eksempel på tabel
Denne tabel indeholder højdefordelingen mellem 20 basketspillere.
| Højde \( ]x_{i-1};x_i] \) |
Antal \( h(x) \) |
Frekvens \( f(x) \) |
Interval midtpunkt \( m(x) \) |
|---|---|---|---|
| \( ]160;170] \) | \( 3 \) | \( 0,15 \) | \( 165 \) |
| \( ]170;180] \) | \( 9 \) | \( 0,45 \) | \( 175\) |
| \( ]180;190] \) | \( 4 \) | \( 0,2 \) | \( 185 \) |
| \( ]190;200] \) | \( 4 \) | \( 0,2 \) | \( 195 \) |
| \( ]200;210] \) | \( 1 \) | \( 0,05 \) | \( 205 \) |
Antal observationer
Interval midtpunkt
Middelværdi (gennemsnit)
1)
2)
For en population er formlen:
1)
2) ( da: \( f_i = \frac{1}{n} \cdot h_i \) )
For en stikprøve
Spredning/standardafvigelse
For en population:
For en stikprøve:
Finans
Generelle betegnelser
- \( n \) er antallet af terminer
- \( K_n \) er kapitalen efter \( n \) terminer
- \( K_0\) er startkapitalen
- \( r \) er renten per termin
- \( y \) er ydelsen per termin
Nutidsværdi: Den værdi et lån/opsparing har lige nu.
Fremtidsværdi: Den værdi et lån/opsparing har efter den aftalte løbetid.
Rentes rente
\( K_n = K_0 \cdot (1+r)^n \)Nutidsværdien
\( K_0 \) udregnes på følgende måde:
1)
2)
Rente
Antal terminer
Effektiv rente
Gennemsnitlig rente
... hvor \( r_x \) er renten i den gældende termin.
Annuitet
Fremtidsværdien
Nutidsværdien
Ydelsen
1) Hvis vi kender \( A_n \)
2) Hvis vi kender \( A_0 \)
Antal terminer
1) hvis vi kender \( A_n \)
2) hvis vi kender \( A_0 \)